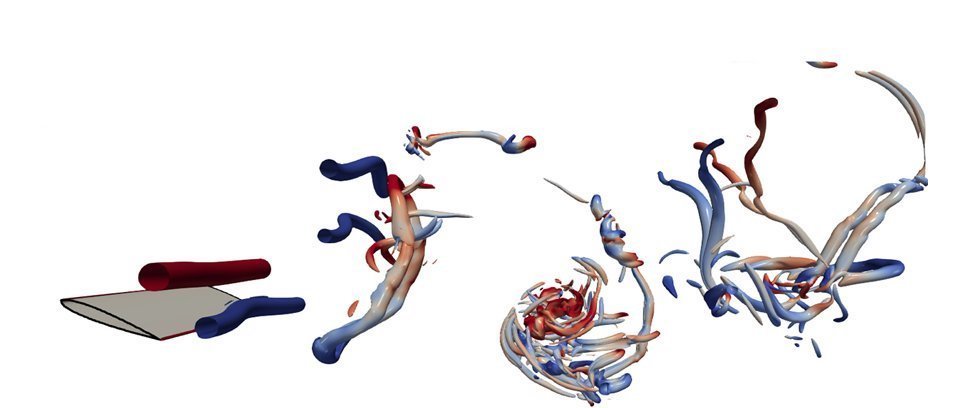
The prevalence of streamwise coherent motions and their role in energy growth, momentum transfer and the self-sustaining processes underlying wall-bounded turbulence, has motivated the development of reduced order representations that emphasize streamwise coherent motion. In the restricted nonlinear (RNL) modeling paradigm, this emphasis is embedded into the decomposition of the dynamics into a streamwise constant mean flow, that is viewed as the large-scale component, and small-scale perturbations about this mean. Order reduction is achieved through a restriction of the nonlinear interactions to those contributing to this large-scale mean. RNL simulations have been shown to produce self-sustaining turbulent activity with low-order statistics, structural features and energetics consistent with moderate Reynolds number canonical wall-bounded turbulent flows at vastly reduced computational costs. In this talk we highlight recent extensions of the RNL model to temporally developing boundary layers. Wall-resolved RNL large eddy simulations of temporally developing boundary layers over walls with constant, increasing and decreasing velocity are performed. The results demonstrate that RNL simulations over an accelerating, decelerating and a uniform velocity wall produce comparable statistical behavior to direct numerical simulations (DNS) of spatially developing flows subject to favorable, adverse and zero pressure gradients. We then focus on the decelerating wall configuration, where significant changes to the structural features, turbulence statistics, and energy spectra are observed as the rate of deceleration is increased. This setting also reproduces the growing extended wake regions in the mean velocity profiles, and the development of an outer layer peak in the second order statistics seen with increasingly adverse pressure gradient boundary layers. These results demonstrate that simulations of RNL flow over decelerating walls capture the key characteristics of adverse pressure gradient flows, and highlight the model’s potential as a computationally efficient means of exploring developing flows that are prevalent in a wide range of applications.

Biography

Dennice F. Gayme is a Professor in Mechanical Engineering at Johns Hopkins University. She received her B. Eng. & Society in Mechanical Engineering from McMaster University in 1997, an M.S. in Mechanical Engineering from the University of California at Berkeley in 1998, and her Ph.D. in Control and Dynamical Systems from the California Institute of Technology in 2010. Her research interests are in modeling, analysis and control of spatially distributed and large-scale networked systems, such as wind farms, wall-bounded shear flows, and power systems. She was a recipient of a JHU Catalyst Award in 2015, ONR Young Investigator and NSF CAREER awards in 2017, a Whiting School of Engineering Johns Hopkins Alumni Association Excellence in Teaching Award in 2020, and the Turbulence and Shear Flow Phenomena (TSFP12) Nobuhide Kasagi Award in 2022. She is a fellow of the American Physical Society (APS) and serves as a Member-At-Large in the Executive Committee of the APS Division of Fluid Dynamics (APS/DFD), the Standing Chair of the Women in Control Committee of the Control Systems Society (CSS) of the IEEE, and on the editorial boards of the Annual Review of Fluid Mechanics, Physical Review Fluids and PRX Energy.